Sunday, December 31, 2017
Saturday, December 30, 2017
Watching The Arctic Die - 3
 |
| Fig. 1 Polar Vortex Fragmentation |
Like the ghost water issue, I have written about this ongoing Polar Vortex disintegration we are now watching and feeling (Watching The Arctic Die, 2).
The reality is that the Arctic Polar Vortex continues to suffer pieces breaking off into smaller pieces in winter time (in fact I was watching the Weather Channel a few minutes ago while they were talking about "two pieces" of the vortex causing extreme cold in the U.S.A. even as we blog ... "when this warm air flows north like this it splits the polar vortex into several pieces in some cases" - Dr. Gregg Postel).
 |
| Fig. 2 Arctic Ice Conditions 29 Dec 17 |
This record low sea ice extent in the Arctic is taking place as we here in "the states" are and have been seeing record cold in some places.
Even the President, a climate change denier, noticed and mentioned that it would be ok to have some "global warming" to ease the coldness.
These very cold pieces of the Arctic Polar Vortex separate or break off then flow south until they meld and blend into the warmer air until equilibrium takes place (e.g. Second Law of Thermodynamics).
I have mentioned this here on Dredd Blog for several years, in various contexts:
The strife caused by the extreme weather is being blamed on a “polar vortex", a spinning wind that in normal years has a beneficial effect in that it keeps sub-zero air trapped above the North Pole. A weakened polar vortex has allowed the trapped air to spill out of the Arctic and hurtle south in an anti-clockwise movement across the face of the US.(The Damaged Global Climate System , On The Origin of Tornadoes - 5, On The Origin of Tornadoes - 6). Record low sea ice extent and record cold areas in the U.S. are symptoms of damage to the global climate system by global warming.
Just why the polar vortex has proved to be too weak to contain the cold air this winter will be a matter for intense scientific study and debate for some time to come. The phenomenon might in large part be explained by the natural changes in climate that occur in the Arctic in winter, including the North Atlantic Oscillation that has a dominant impact on wind patterns and storm tracks in the region.
But Noaa, a federal agency, has also floated the possibility that a reduction in summer sea ice cover caused by climate change could be a factor behind the weakening of the polar vortex. That would have the paradoxical effect that while Arctic waters are getting warmer, North America experiences much colder snaps such as the present severe weather as a result of Arctic air spilling out from the North Pole and moving south.
A mechanism to explain how the behavior of the stratosphere may affect tropospheric weather patterns has been proposed by scientists at theUniversity of Illinois. If correct, the idea could be included in models to better understand the climate system and predict the weather.
Normal polar vortex
“Recent observations have suggested that the strength of the stratospheric polar vortex influences circulation in the troposphere,” said Walter Robinson, a UI professor of atmospheric sciences. “We believe there is a weak forcing in the stratosphere, directed downward, that is pinging the lower atmosphere, stimulating modes of variability that are already there.”
The polar vortex is a wintertime feature of the stratosphere. Consisting of winds spinning counterclockwise above the pole, the vortex variesin strength on long time scales because of interactions with planetary waves global-scale disturbances that rise from the troposphere. “The polar vortex acts like a big flywheel,” Robinson said. “When it weakens, it tends to stay weakened for a while.”
At (d) a piece breaks away
Other researchers have noted a statistical correlation between periods when the polar vortex is weak and outbreaks of severe cold in many Northern Hemisphere cities.
“When the vortex is strong, the westerlies descend all the way to Earth's surface,” Robinson said. “This carries more air warmed by the ocean onto the land. When the vortex is weak, that's when the really deep cold occurs."
Under normal climate conditions, cold air is confined to the Arctic by the polar vortex winds, which circle counter-clockwise around the North Pole. As sea ice coverage decreases, the Arctic warms, high pressure builds, and the polar vortex weakens, sending cold air spilling southward into the mid-latitudes, bringing record cold and fierce snowstorms. At the same time, warm air will flow into the Arctic to replace the cold air spilling south, which drives more sea ice loss.
The next post in this series is here, the previous post in this series is here.
Ode to Pruitt, Trump & Inhoff, Inc.
Friday, December 29, 2017
The Machine Religion - 2
by Vachel Lindsay
“There’s machinery in the
butterfly;
There’s a mainspring to the
bee;
There’s hydraulics to a daisy,
And contraptions to a tree.
If we could see the birdie
That makes the chirping sound
With x-ray, scientific eyes,
We could see the wheels go
round.
And I hope all men
Who think like this
Will soon lie
Underground."
The next post in this series is here, the previous post in this series is here.
Tuesday, December 26, 2017
On Thermal Expansion & Thermal Contraction - 30
 |
| Fig. 1 |
 |
| Fig. 2 |
In recent posts in a recent series I pointed out that "golden" locations have been discovered and used in sea level measurement scenarios (PSMSL) and surface atmospheric measurement scenarios (GISTEMP) but not for WOD datasets.
What was missing was the "golden" for World Ocean Database measurements (WOD).
During that exercise I discovered that the Dredd Blog seven level depth system did not sync well with the WOD Thirty-Three Level depth system (Oceans: Abstract Values vs. Measured Values, 2, 3, 4, 5, 6, 7).
 |
| Fig. 3a |
 |
| Fig. 3b Zones Used @ Pairs |
So, I changed (databases and software) to the thirty-three depth level system (the graphs at Fig. 1 and Fig. 2 show the quantity of measurements in the CTD & PFL WOD datasets at each of the 18 WOD Layers (0-17) and at each of the 33 depths (0-5500).
Another issue was that during the year I switched to using the TEOS-10 toolkit for thermal expansion calculations, which required specialized measurement usage.
The reason for this requirement is that TEOS calculations require a pair of measurements, that is, one member of the pair must be in situ T (temperature), and the other member of the pair must be in situ SP (salinity).
 |
| Fig. 4 Zones Used @ Singles |
That pair requirement decreases the number of measurements that can be used to calculate the TEOS values, because the datasets have varying numbers of single measurements.
When the TEOS-10 toolkit is used those software functions generally require salinity, temperature, and depth values from the same time and depth in order to render a valid result (especially those associated with calculating thermal expansion and contraction).
 |
| Fig. 5 |
What causes that can be grasped by looking at the measurement totals in the graphic at Fig. 5.
All of those in situ measurement numbers that end in an odd number are not composed completely of pairs.
Many are single measurements of either salinity or temperature, but not both, at a given depth, thus those measurement singularities cannot be used when calculating thermosteric sea level or ocean volume changes values with the TEOS-10 toolkit.
For that matter generally, any other TEOS values which require paired in situ measurements can't be calculated with a single temperature measurement or a single salinity measurement.
As it turns out, the Zones that contain pair-measurements (Fig. 3b) end up being the "Golden 271" Zones for purposes of thermosteric calculations, while the larger numbered list of Zones (Fig. 5) can and must be used for other purposes.
NOTE: the "measurements" mentioned and counted are from the "secondary datasets" which are mean averages of the 0.9 billion in situ measurements in the primary datasets (e.g. the 59,218 "measurements" @ Layer 9 in Fig. 5 are 59,218 mean averages of data in the primary datasets ... as are all other "measurements" mentioned in this post).
In conclusion, I hope that eventually the establishment scientific community begins to look into the roots of the beginning of the misconceptions about thermal expansion hypotheses that allege but do not prove that thermal expansion is the major factor in sea level change.
The next post in this series is here, the previous post in this series is here.
Sunday, December 24, 2017
Saturday, December 23, 2017
Oceans: Abstract Values vs. Measured Values - 7
 |
| Fig. 1 |
Today's graphs are the culmination of the software module upgrade and database restructuring.
 |
| Fig. 2 |
 |
| Fig. 3 |
That "Golden" totals to 217 Zones taken from all WOD layers containing data, (today's graphs are all from that dataset).
 |
| Fig. 4 |
Not using the fences increases the resolution so that you can see glimpses of both the T pattern and the CT pattern individually at several places.
The graph at Fig. 2 is the exact same data with the fences included.
I included both graph types so you can see that the calculated TEOS CT is quite close to the in situ measurement values (T), but they are not exactly the same.
The graph at Fig. 3 once again reaffirms that the Absolute Salinity (SA) and the in situ salinity measurement, Practical Salinity (SP), vary more than the T and CT temperatures do.
As I indicated in a recent post (On Thermal Expansion & Thermal Contraction - 29), that is to be expected because SP involves measuring by ascertaining conductivity, while SA involves calculating mass (H2O and non-H2O content) factors.
 |
| Fig. 5 WOD Zones with in situ data (blue squares) |
The expansion / contraction pattern ends at 4.82% (8.92699 ÷ 185.157 = 0.048213084 ... 4.82%) of the PSMSL sea level value as recorded by tide gauge stations.
Regular readers know that for years Dredd Blog calculations of thermal expansion were based on a 5.1% value for thermal expansion (e.g. On Thermal Expansion & Thermal Contraction).
That 5.1% was the percent left over after accounting for ice sheet loss (melt-water increase) and ghost water (gravity-held ocean water release) relocation (NASA Busts The Ghost).
The previous post in this series is here.
Lyrics to "25 Or 6 To 4"
Thursday, December 21, 2017
On Thermal Expansion & Thermal Contraction - 29
 |
| Fig. 1a |
 |
| Fig. 1b |
 |
| Fig. 1c |
 |
| Fig. 1d |
 |
| Fig. 1e |
 |
| Fig. 1f |
 |
| Fig. 1g |
 |
| Fig. 1h |
 |
| Fig. 1i |
 |
| Fig. 2a |
 |
| Fig. 2b |
 |
| Fig. 2c |
 |
| Fig. 2d |
 |
| Fig. 2e |
 |
| Fig. 2f |
 |
| Fig. 2g |
 |
| Fig. 2h |
 |
| Fig. 2i |
I. Background
I finally came up for air after redesigning my SQL tables.
As regular readers know, traditionally I have used seven depth levels of the ocean, while the WOD manual uses 33 depth levels.
So, I changed the SQL tables to hold 33 depth levels rather than seven, and rebuilt the tables.
Which necessitated redoing the software to accommodate those changes.
A perplexing development in the world of graphing ocean dynamics emerged as I mentioned in the previous post (On Thermal Expansion & Thermal Contraction - 28) and two other posts further explaining the issue (see e.g. Oceans: Abstract Values vs. Measured Values - 6).
Some of the problem developed because I was using two depth level models; one used seven levels, the other thirty three depth levels.
It was not accurate enough that way, so I went the way of the WOD manual, and adjusted the databases and software modules accordingly.
II. Redesign Issues
While planning a strategy it dawned on me that the processing of the work of scientists (who worked hard to gather the billions of measurements they make available to us) should be like human governments (from the bottom up).
So, the processing of the salinity and temperature data begins at the deepest depth that the measurements were taken at, and then works up to the surface level from there.
It follows the natural flow of a warming world in the sense that as the processing moves up through the depth levels, the ocean temperatures are generally warming.
Having changed the number of depth levels from seven to thirty three, it also changed the quantity of water associated with each depth level.
I process each of the thirty ocean basins separately because they have different temperature highs and lows at each depth level.
So, the volume of water at each depth level is smaller, which works to increase accuracy quite a bit.
I consider and process each depth level as if it was the entire ocean in the sense that there is a consistent volume of water, but the pressure, temperature, and salinity tends to be different at each depth level.
When the software processing reaches the final level (0-10 meters in depth), I add up the recorded salinity, temperature, and thermal expansion and contraction values, taken from each depth level on the way up.
That has to be done for each ocean basin (WOD zone by WOD zone) because the latitude and longitude contribute significantly to the results.
The latitude and longitude values are parameters in some of the critical TEOS formulas, so the use of small zones and levels increases the accuracy of several results.
Another factor that improved the functionality and the results was using the same logic to calculate the Abstract Maximum and Minimum values as well as the WOD measured values.
That results in a synchronization which removed the inconsistency in thermal expansion results compared to temperature and salinity results.
They are all now in sync as the graphs in today's post show.
All of the categories fit well within the maximum and minimum parameters which are taken from the WOD manual @ Appendix 11.
III. The Why Of It
This series explores the realm of the hypotheses of thermal expansion of the oceans as the global climate system gyrates to the increases in global warming.
The foundational statement is usually "water expands as it is heated" without mentioning that "water shrinks as it is heated" because each of those two eventualities depends on the temperature of the water at the time the heat is added to the water (On Thermal Expansion & Thermal Contraction).
That discrepancy inspired me to look closer and deeper into the subject, as this series details.
Along the way I discovered that one can get a completely different picture of the ocean depending on where one takes measurements.
Today's graphs show how different patterns emerge depending on what segment or section of ocean measurements one uses.
That does not mean that the measurements are wrong, it means that one must use a balanced selection of measurements.
It is like having five different thermometers in a house where there are different temperatures inside.
The temperature in the garage, a closet, inside the refrigerator, in the basement, and in the attic will render different temperatures.
That is why the thermometer that controls the heating and cooling systems has to be strategically located.
The same goes for determining general global conditions of the oceans as they absorb global warming.
IV. Additional Feature Issues
To give us another advantage to use in our ongoing quest about the facts and fantasies of thermal expansion, I added additional WOD layer processing along with additional WOD zone processing while I was modifying the software modules.
A separate functionality class contains lists of layers as well as lists of individual zones (which can be easily changed).
The current configuration allows the processing of six "golden layers", six "golden zones", eight "golden layers", eight "golden zones", as well as processing 117 zones and processing all 18 WOD layers.
The reason for these differences is because I am searching for what has already been found for tide gauge stations and weather stations.
I am talking about a representative few examples which one can look at to get the big picture.
V. The Graphs
The graphs today come in two sections.
One is the layers section (Fig. 1a - Fig. 1i, left side), and the other is the zones section (Fig. 2a - Fig. 2i, right side).
The use of layers (36 zones per layer) arguably has the advantage of being in sync with the natural temperature bands, beginning at the warmest band at the equator, then moving towards the gradually cooling bands as the layers proceed toward the coldest band at the poles.
The use of lists of zones allows one to be a bit more selective.
One way or the other, we should be able to find the Goldilocks "just right" configuration to use to inform us of an accurate, broader picture (like tide gauge and weather station configurations do).
VI. Granularity
I noticed that the TEOS calculations give a tighter group in the temperature processing than they do in the salinity processing.
Notice that the salinity patterns in Fig. 1a - Fig. 1c tend to produce two visible lines, while the temperature related graphs at Fig. 1d - Fig. 1f look as if they produce the same line (i.e. only one line).
That is not the case, it is just that the numbers are different @ the temperature graphs (T compared to CT), but they are not different enough to make two visibly discernible lines at this resolution.
Conservative Temperature (CT) and Absolute Salinity (SA) are TEOS concepts, however, of the two, SA, is the more revolutionary departure from "40 years of error" when scientists were using conductivity as the proper measure of salinity.
So, the smaller difference between in situ temperature (T) measurements and calculated Conservative Temperature (CT) values, compared to the larger difference between in situ salinity (SP) measurements and calculated Absolute Salinity (SA) values, is not a great surprise.
VII. Conclusion
We can now move forward into finding out why thermal expansion has been misused.
And we can do so on "the same page" that has only 33 depths for all purposes, instead of trying to patch a 7 depth system and a 33 depth system together.
The next post in this series is here, the previous post in this series is here.
Thursday, December 14, 2017
Oceans: Abstract Values vs. Measured Values - 6
 |
| Fig. 1 |
 |
| Fig. 2 |
 |
| Fig. 3 |
 |
| Fig. 4 |
 |
| Fig. 5 |
 |
| Fig. 6 |
The post showed thermosteric sea level changes that were out side those boundaries, so I began to look into the matter.
The graphs posted (Fig. 1 - Fig. 6) show that WOD in situ temperature measurements are not the problem.
All of the various in situ measurements, TEOS Conservative Temperature (CT) calculations, and Abstract maximum / minimums calculations show that the WOD measurements are within bounds.
It remains to be seen what the problem with the thermosteric sea level changes that were out of bounds is caused by.
I am still researching the issue to determine if it is a TEOS or Dredd Blog bug concerning thermosteric volume calculations.
I will update this series accordingly when I know more.
I moved things around in Fig. 1 so you can see the colors of the Abstract Maximum / Minimum lines (the long ones from 1880 - 2016).
The WOD in situ and CT lines are short red and black lines spanning 1968 - 2016 (right hand side of the graphs).
The Abstract maximum and minimum abstract CT lines are greenish, while the middle (average) abstract CT line is blue.
As you can see, the various configurations of layers and zones are reasonably within the confines of the maximum / minimum ranges.
The salinity measurements were out of bounds (higher than the maximum) so I am checking that out prior to posting the Absolute Salinity graphs.
I am checking the source code closely to see if there is a logical error that would make the salinity go out of bounds.
Even though I doubt that a two or three g/kg value above the maximum, which is what the salinity is showing, would cause the sea level gyrations in the previous post, I am looking closely at all of that.
I suspect that it is more likely to be a TEOS issue, because both the thermosteric volume and the thermosteric sea level gyrations are related.
The next post in this series is here, the previous post in this series is here.
Wednesday, December 13, 2017
Monday, December 11, 2017
Oceans: Abstract Values vs. Measured Values - 5
 |
| Fig. 1 Abstract maximum, average, and minimum |
I mean where those papers pointed out how the measurements which scientists have been able to take are not spread out evenly (in terms of latitude & longitude) across the vast oceans of the world.
My argument or discussion about this is that we need to have a way of doing with WOD datasets what the GISTEMP and PSMSL data users have been able to do with those datasets.
 |
| Fig. 2a |
 |
| Fig. 2b |
 |
| Fig. 2c |
That is, to define which WOD layers and/or zones can be used to represent the entirety of the ocean conditions, that is, the oceans as a whole.
Only twenty-three PSMSL tide gauge stations out of about 1,400 tide gauge stations can do that in terms of sea level change.
The GISTEMP is similar in that the global mean average temperature anomaly can be shown in the same manner (a representative subset).
But, as those papers discussing the world oceans point out, the same is not yet accomplished with WOD datasets.
The measurements are too concentrated in certain areas to the exclusion of other areas, are too few, and do not go deep enough into the abyss.
The ARGO automated system of submarine drones is changing that in the upper 2,000 m of the oceans, but that is a relatively recent technological win.
There is no long term in situ set of measurements of ocean temperature and salinity data going back in time for over a century, like there are with the PSMSL and GISTEMP datasets.
To visually point out the measurement aberrations I am speaking of, let's look at the new graphs generated by version 1.7 of the software I am constructing.
The graph at Fig. 1 shows the ABSTRACT (calculated) maximum, average, and minimum thermal expansion and contraction pattern from the years 1880 to 2016.
The three graphs at Fig. 2a - Fig. 2c show what happens when in situ WOD measurements are added to the data stream used to generate those abstract graphs.
 |
| Fig. 3 Abstract avg. compared to measured |
Since those values from the WOD manual define validity at all ocean basins and all depths at those basins, being out of sync with them is a problem, especially when the out-of-sync pattern emerges using any of the three different sets of WOD data which compose three different layer lists.
Those three sets are 1) all layers, 2) 6 selected layers, and 3) 8 selected layers, as shown by the report below.
The software module loading sequence proceeds from 1 through 6 (GISS data loader, ABSTRACT data generator, G6 loader, PSMSL loader, G8 loader, and the WOD all-layers loader.
Those modules load in situ measurement data from SQL tables, as well as WOD maximum / minimum valid values.
The software then organizes the data into annual structures (past to present).
The measured values are converted into TEOS values, according to the TEOS rules, by functions in the TEOS toolkit (e.g. Golden 23 Zones Meet TEOS-10).
I may have to stop using WOD layers, to instead use individually selected WOD Zones.
I want to find locations that stay within the guard rails of the valid WOD maximum / minimum values in Appendix 11 of their user manual (see links here).
I am on the case.
The next post in this series is here, the previous post in this series is here.
A printout of the loading sequence of the module follows:
GISS, PSMSL, WOD & TEOS
Data Analyzer Report
(ver. 1.7)
=======================
(1) GISS Loader
---------------
processed 137 rows
(2) ABSTRACT Calculator
-----------------------
processed:
137 years of data
30 ocean basins
at 33 depths
(3) WOD G6 Loader
-----------------
processing layer 5
processed 118 rows
(59 years) of data
processing layer 7
processed 102 rows
(51 years) of data
processing layer 8
processed 162 rows
(81 years) of data
processing layer 9
processed 176 rows
(88 years) of data
processing layer 10
processed 172 rows
(86 years) of data
processing layer 12
processed 142 rows
(71 years) of data
(4) PSMSL Loader
----------------
processed 10,199 rows
(5) WOD G8 ALT Loader
---------------------
processing layer 3
processed 142 rows
(71 years) of data
processing layer 5
processed 118 rows
(59 years) of data
processing layer 7
processed 102 rows
(51 years) of data
processing layer 8
processed 162 rows
(81 years) of data
processing layer 9
processed 176 rows
(88 years) of data
processing layer 10
processed 172 rows
(86 years) of data
processing layer 12
processed 142 rows
(71 years) of data
processing layer 14
processed 142 rows
(71 years) of data
(6) WOD Loader (all layers)
---------------------------
processing layer 0
processed 60 rows
(30 years) of data
processing layer 1
processed 118 rows
(59 years) of data
processing layer 2
processed 96 rows
(48 years) of data
processing layer 3
processed 142 rows
(71 years) of data
processing layer 4
processed 188 rows
(94 years) of data
processing layer 5
processed 118 rows
(59 years) of data
processing layer 6
processed 178 rows
(89 years) of data
processing layer 7
processed 102 rows
(51 years) of data
processing layer 8
processed 162 rows
(81 years) of data
processing layer 9
processed 176 rows
(88 years) of data
processing layer 10
processed 172 rows
(86 years) of data
processing layer 11
processed 142 rows
(71 years) of data
processing layer 12
processed 142 rows
(71 years) of data
processing layer 13
processed 144 rows
(72 years) of data
processing layer 14
processed 142 rows
(71 years) of data
processing layer 15
processed 156 rows
(78 years) of data
processing layer 16
processed 102 rows
(51 years) of data
processing layer 17
processed 0 rows
(0 years) of data
Friday, December 8, 2017
Oceans: Abstract Values vs. Measured Values - 4
 |
| Fig. 1a |
 |
| Fig. 1b |
I. Background
This series is about what to do about the dearth of in situ measurements of the whole ocean, top to bottom (Oceans: Abstract Values vs. Measured Values, 2, 3).
The issue, including what to do about it, has been addressed in the scientific literature:
"Prior to 2004, observations of the upper ocean were predominantly confined to the Northern Hemisphere and concentrated along major shipping routes; the Southern Hemisphere is particularly poorly observed. In this century, the advent of the Argo array of autonomous profiling floats ... has significantly increased ocean sampling to achieve near-global coverage for the first time over the upper 1800 m since about 2005. The lack of historical data coverage requires a gap-filling (or mapping) strategy to infill the data gaps in order to estimate the global integral of OHC."(Ocean Science 2016, Cheng et alia, emphasis added; PDF here). Going back a bit further, the issue came up in another paper:
"A compilation of paleoceanographic data and a coupled atmosphere-ocean climate model were used to examine global ocean surface temperatures of the Last Interglacial (LIG) period, and to produce the first quantitative estimate of the role that ocean thermal expansion likely played in driving sea level rise above present day during the LIG. Our analysis of the paleoclimatic data suggests a peak LIG global sea surface temperature (SST) warming of 0.7 ± 0.6°C compared to the late Holocene. Our LIG climate model simulation suggests a slight cooling of global average SST relative to preindustrial conditions (ΔSST = −0.4°C), with a reduction in atmospheric water vapor in the Southern Hemisphere driven by a northward shift of the Intertropical Convergence Zone, and substantially reduced seasonality in the Southern Hemisphere. Taken together, the model and paleoceanographic data imply a minimal contribution of ocean thermal expansion to LIG sea level rise above present day. Uncertainty remains, but it seems unlikely that thermosteric sea level rise exceeded 0.4 ± 0.3 m during the LIG. This constraint, along with estimates of the sea level contributions from the Greenland Ice Sheet, glaciers and ice caps, implies that 4.1 to 5.8 m of sea level rise during the Last Interglacial period was derived from the Antarctic Ice Sheet. These results reemphasize the concern that both the Antarctic and Greenland Ice Sheets may be more sensitive to temperature than widely thought."(The role of ocean thermal expansion, AGU, emphasis added). Basically, the scientists point out that this exercise is not a picnic:
"The oceans present myriad challenges for adequate monitoring. To take the ocean’s temperature, it is necessary to use enough sensors at enough locations and at sufficient depths to track changes throughout the entire ocean. It is essential to have measurements that go back many years and that will continue into the future.(The Most Powerful Evidence, Inside Climate News, emphasis added). That quote contains a reference to "Cheng et al. 2017" which contains the following statement:
...
Since 2006, the Argo program of autonomous profiling floats has provided near-global coverage of the upper 2,000 meters of the ocean over all seasons [Riser et al., 2016]. In addition, climate scientists have been able to quantify the ocean temperature changes back to 1960 on the basis of the much sparser historical instrument record [Cheng et al., 2017]."
"In this paper, we extend and improve a recently proposed mapping strategy (CZ16) to provide a complete gridded temperature field for 0- to 2000-m depths from 1960 to 2015.(Improved estimates of ocean heat content from 1960 to 2015, Cheng et al, 2017). In other words, it has not yet been accomplished.
...
The success of a mapping method can be judged by how accurately it reconstructs the full ocean temperature domain. When the global ocean is divided into a monthly 1°-by-1° grid, the monthly data coverage is [less than]10% before 1960, [less than]20% from 1960 to 2003, and [less than]30% from 2004 to 2015 (see Materials and Methods for data information and Fig. 1)."
That is where the Dredd Blog criticism of "thermal expansion is the major cause of sea level rise in the past century or so" comes from (On Thermal Expansion & Thermal Contraction, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27).
II. An Abstract Observation
Now, let's consider that "gap-filling (or mapping) strategy" exercise (mentioned in the last quote above, Cheng et al, 2017).
The problem has been approached here at Dredd Blog by developing a software program I call an abstract pattern generator. which produces WOD patterns using data in the WOD documentation.
 |
| Fig. 2a |
 |
| Fig. 2b |
The upper pane of Fig. 1a is a graph generated from data of the Permanent Service for Mean Sea Level (PSMSL).
It details sea level rise (SLR) at the "Golden 23" tide gauge stations (185.157 mm of SLR).
The lower pane is a graph of the abstract pattern of thermal expansion over the same time frame (25.019 mm of SLR).
In other words, the abstract thermal expansion pattern shows that thermal expansion is only 13.5% of total SLR (25.019 ÷ 185.157 = 0.135123166 or 13.5%) during that time frame, which means that it is not a major portion of global sea level rise, because those numbers also mean that 86.5% of SLR is caused by ice sheet and land glacier melt water.
The abstraction calculation is based on World Ocean Database (WOD) data in their official documentation, depicted in part at Fig. 2a and Fig. 2b, which is a portion of "APPENDIX 11. ACCEPTABLE RANGES OF OBSERVED VARIABLES AS A FUNCTION OF DEPTH, BY BASIN" (see Appendix 11, page 132, of The WOD Manual, PDF).
The gist of Appendix 11 is to show maximum and minimum values at all ocean depths in all ocean basins around the globe.
By adding the maximum and minimum values together, then dividing by 2 (at each depth of each ocean basins), the software is then ready for the next step, which is to conform those values to GISTEMP constraints.
By "GISTEMP constraints" I mean adjusting those mean average Appendix 11 values by the GISTEMP anomaly pattern.
That is done by multiplying the WOD values by 0.93 (93% of that GISTEMP anomaly value becomes the temperature anomaly value in each ocean basin at each depth).
That is because scientists tell us that some 93% of heat trapped by green house gases ends up in the oceans.
So, by fusing that GISTEMP anomaly pattern to the abstract temperature pattern made by the WOD data, we have a pattern which we can use to generate Thermodynamic Equation Of Seawater (TEOS) patterns (e.g. Golden 23 Zones Meet TEOS-10).
III. Using Abstract Patterns With TEOS-10
Using abstract WOD data to generate TEOS values is done by the same process as using in situ ocean temperature and salinity measurements (The Art of Making Thermal Expansion Graphs).
To conform either in situ temperature and salinity measurements or abstract temperature and salinity values, one uses the TEOS functions (the difference is that the abstract values have been conformed to the GISTEMP pattern as stated in Section II above).
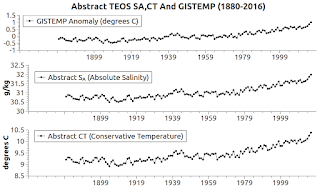
The graph at Fig. 1b shows the resulting TEOS Conservative Temperature (CT) and Absolute Salinity (SA) patterns that emerge on an annual basis from 1880 - 2016 when one uses this technique.
From that, we then can then generate the thermal expansion coefficient and the thermosteric volume change.
From that thermosteric volume change we can calculate the sea level change (SLC) as shown in Fig. 1a.
Using the WOD manual data for all 30 ocean basins around the globe, and all 33 depths in each of those ocean basins, forms a pattern against which we can judge the general completeness and general accuracy of our in situ measurements.
It also helps us to select a "Golden 23" group of areas that mirror the whole ocean (On Thermal Expansion & Thermal Contraction - 28).
IV. Comparing In Situ Measurement Patterns
With Abstract Calculated Patterns
With Abstract Calculated Patterns
So now we can talk about the current techniques of using what is described as skimpy in situ measurements (down to only about 2,000 m depth, when the average ocean basin depth is 3,682.2 m ... ~50% not used) to do the estimations all of the science team authors wrote about.
They pointed out that we have to use estimations in any case, because the datasets are incomplete in various places for various reasons, from dangerous conditions to weaker technology in times past.
To me, incomplete data is a bad place to start, having realized that the in situ measurements, although quite accurate and plentiful, are a patchwork of convenience-based expeditions that can make it difficult to see the entire picture.
I mean the total picture which must be constructed from outside the convenience zone of only expeditions to safe and warm global ocean areas.
That is why I hypothesize that it is better to start with an abstract pattern which matches the pattern made by our historically complete datasets (e.g. GISTEMP & PSMSL).
V. Conclusion
"He say one and one and one is three ... come together ..."
The next post in this series is here, the previous post in this series is here.
Subscribe to:
Posts (Atom)



