 |
| Fig. 1 WOD Layers (0-17) |
This module works on WOD layers as shown by the graphic at Fig. 1.
Some results, in terms of mean average, are shown on the graph at Fig. 2 (just so you know, the ending sea level rise values show that thermal expansion was 2.37% of the total sea level rise).
 |
| Fig. 2 Sea level change |
Thermal expansion was 2.62688 mm, while total sea level rise as measured at tide gauge stations around the globe was 110.855 mm (the percentage arithmetic is: 2.62688 ÷ 110.855 = 0.023696541 = 2.37%).
The graphs at Fig. 3 - Fig. 19 detail the mean average of each WOD layer's thermal expansion & contraction at each Zone in each layer (Fig. 1 shows the zones in each layer).
I had never graphed those measured values going that far back (1800's) before, because the WOD CTD and PFL datasets I used did not go back past the 1960's.
I began to use all WOD Datasets a while back, so the 1800's can now be done (Databases Galore - 22, 23, 24, and 25).
 |
| Fig. 3 Layer 0 |
 |
| Fig. 4 Layer 1 |
 |
| Fig. 5 Layer 2 |
 |
| Fig. 6 Layer 3 |
 |
| Fig. 7 Layer 4 |
 |
| Fig. 8 Layer 5 |
 |
| Fig. 9 Layer 6 |
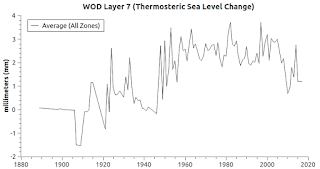 |
| Fig. 10 Layer 7 |
 |
| Fig. 11 Layer 8 |
 |
| Fig. 12 Layer 9 |
 |
| Fig. 13 Layer 10 |
 |
| Fig. 14 Layer 11 |
 |
| Fig. 15 Layer 12 |
 |
| Fig. 16 Layer 13 |
 |
| Fig. 17 Layer 14 |
 |
| Fig. 18 Layer 15 |
 |
| Fig. 19 Layer 16 |
Since the GISS atmospheric temperature declines as one goes back in time, so did my estimation of ocean temperatures.
The measured values we now have do not follow that computed pattern.
Compare "On Thermal Expansion & Thermal Contraction - 19", at Fig. 2 therein, with "On Thermal Expansion & Thermal Contraction - 37", at Fig. 3c therein.
The older measurements defied my declining temperature expectations and logic as to past temperatures.
As we go back in time far enough the measurements made then were probably not taken at some of the locations they are routinely taken at now (e.g. ARGO floats).
Nor were measurements taken at deep-depths where water in non-polar zones is generally cooler.
Wooden sailing ships and even coal fired steamers had limited ocean access due to weather conditions and traveling time required.
Fuel, food, fresh water, and other supplies only lasted so long.
So, either there were technical difficulties with gathering data in extreme or far away places, or the ocean temperature trends then are contrary to our more recent observations and measurements of trends.
I doubt the latter ("ocean was different then"), because sea level change, as measured by tide gauge stations going back to the 1700's, indicates that warming has increased since the late 1700's because melting has increased since then (Proof of Concept, 2, 3, 4, 5, 6, 7, 8, 9).
The GISS atmospheric temperature measurements at weather stations around the globe also indicate that atmospheric warming has increased just a bit over 1 degree C over that time frame.
How SLC Graphs Are Made
Today's graphs are about thermosteric sea level change.
That is, change brought about by changing ocean temperatures.
The mean average sea level change shown in Fig. 2 was calculated using all PSMSL tide gauge station records and all WOD dataset measurements containing both T (temperature) and SP (salinity) values.
The XBT and MBT datasets are excluded from this exercise.
They do not contain any SP measurements with which to match the T measurements and thereby do TEOS calculations.
Anyway, the procedure is to gather the measurements into an array based on sequential years from 1800 to the present.
That means using values measured from up to 33 depth level sections or slices of varying sizes (10m, 20m, 30m, 50m, 75m, 100m, 125m, 150m, 200m, 250m, 300m, 400m, 500m, 600m, 700m, 800m, 900m, 1000m, 1100m, 1200m, 1300m, 1400m, 1500m, 1750m, 2000m, 2500m, 3000m, 3500m, 4000m, 4500m, 5000m, 5500m, and >5500m).
Note that when calculating thermal expansion both mass-unit (how many molecules) and volume (distance between molecules) must be taken into consideration.
The formula "volume = length times width times height" (v = l * w * h) must be used to calculate individual depth level mass-units because "h" is different at some depth levels.
For example h=10 at depth-level 0 to 10m, but h=500 at depth-level 3500m to 4000m.
Thus, a volume calculation for each of the depth-level mass-units must take place when one is calculating their individual thermal expansion / contraction values.
Not only that, WOD zones themselves have different "w" values because longitude width varies (progressively narrower moving from the equator toward the poles, and vice versa pole to equator).
So, each "cubic" section (depth-level mass-unit) of each zone is calculated independently for volume change caused by temperature change (thermal expansion / contraction).
The process goes like this for each WOD zone and each depth level:
1) calculate the mass-unit of the zone's water column depth level (v=l*w*h);
2) convert T and SP values into TEOS-10 Conservative Temperature (CT) and Absolute Salinity (SA) values;
3) calculate the thermal expansion coefficient (tec) using the TEOS-10 gsw_alpha function;
4) calculate the change in temperature at each depth-level mass-unit from one year to the next (an increase in temperature will generally mean thermal expansion while a decrease in temperature will generally mean thermal contraction);
5) derive the net change in volume ("vc") (not the mass-unit "mu") for each zone at each depth-level:
vc = mu * (1 + ( tec * ct - prev_ct ))6) sum the volume change ("vc") increases and decreases at each depth-level of each zone;
7) to derive a mean average for that layer, sum the "vc" zone changes for each WOD latitude layer, then divide that sum by the number (count) of "vc" values in that latitude layer.
The initial mass-unit ("mu") of each depth level must remain constant throughout the span of years of the calculations, because the thermosteric volume changes (increases and decreases) are the "vc" ... not the "mu" (mass-unit).
The "vc" is what changes from year to year due to thermal changes.
It is important that the "mu" ("l" * "w" * "h") value for each mass-unit (depth-level water quantity) in each zone must not change while doing the thermosteric calculations (note the "l,w,h" example mass-unit for Bathypelagic depth-level @ Fig. 20):
(Journal of Geophysical Research: Oceans, emphasis added). Once the proper techniques are in place, the process is straightforward."A common practice in sea level research is to analyze separately the variability of the steric and mass components of sea level. However, there are conceptual and practical issues that have sometimes been misinterpreted, leading to erroneous and contradictory conclusions on regional sea level variability. The crucial point to be noted is that the steric component does not account for volume changes but does for volume changes per mass unit (i.e., density changes). This indicates that the steric component only represents actual volume changes when the mass of the considered water body remains constant."
Fig. 20 Bathypelagic mass-unit
The next post in this series is here, the previous post in this series is here.

"Major Climate Report Describes a Strong Risk of Crisis as Early as 2040" (link)
ReplyDeleteWow, the IPCC learned some new words like "crisis" ...