 |
| Fig. 1 Thermosterics |
I mean direct calculation by way of in situ measurements of both temperature and conductivity (salinity).
That is because only temperature is recorded in them.
I am talking about the MBT and XBT datasets.
The TEOS-10 functions for calculating thermal expansion require both T (temperature) and SP (practical salinity ... or conductivity) in order to calculate thermal expansion.
The process goes like this: 1) collect the temperature "T" and "SP" (conductivity) at depth "D"; 2) convert SP into Absolute Salinity (gsw_SA_from_SP); and 3) convert "T" into "CT" (gsw_CT_from_t).
That part is quite straightforward, unless of course "SP" is missing, as pointed out in TEOS-10 publications:
"3. Absolute Salinity SA(Getting Started, TEOS-10, PDF). The unique expansion/contraction properties (Fig. 1) of both pure water and seawater can't be fully discerned without an evaluation of Absolute Salinity (SA).
Perhaps the most apparent change in using TEOS-‐‐10 compared with using the International Equation of State of seawater (EOS-‐‐80) is the adoption of Absolute Salinity SA instead of Practical Salinity SP (PSS-‐‐78) as the salinity argument for evaluating the thermodynamic properties of seawater. Importantly, Practical Salinity is retained as the salinity variable that is stored in national databases. This is done to maintain continuity in the archived salinity variable, and also because Practical Salinity is virtually the measured variable (whereas Absolute Salinity is a calculated variable).
The “raw” physical oceanographic data, as collected from ships and from autonomous platforms (e. g. Argo), and as stored in national oceanographic data bases, are
• Practical Salinity (SP , unitless, PSS-‐‐78) andUnder TEOS-‐‐10 all the thermodynamic properties are functions of Absolute Salinity SA (rather than of Practical Salinity), hence the first step in processing oceanographic data is to calculate Absolute Salinity, and this is accomplished by the GSW function gsw_SA_from_SP. Hence the function gsw_SA_from_SP is perhaps the most fundamental of the GSW functions as it is the gateway leading from oceanographic measurements to all the thermodynamic properties of seawater under TEOS-‐‐10. A call to this function can be avoided only if one is willing to ignore the influence of the spatial variations in the composition of seawater on seawater properties ..."
• in situ temperature (t, °C , ITS-‐‐90) as functions of
• sea pressure ( p, dbar ), at a series of
• longitudes and latitudes.
 |
| Fig. 2a MBT Dataset |
 |
| Fig. 2b XBT Dataset |
This series has considered that reality from several viewpoints (On Thermal Expansion & Thermal Contraction, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36).
Nevertheless, today I have displayed the two datasets (MBT, XBT) which contain only "T" (excluding "SP") measurements just to show readers that I do have that data (Fig. 2a - Fig. 2b).
I have also furnished a mean average graph of all "T" measurements in the WOD Datasets (Fig. 3c); a comparison of mean average "T" values to MBT measurements of "T" (Fig. 3a); and finally the same comparison with respect to XBT (Fig. 3b).
 |
| Fig. 3a Mean Average (during MBT years) |
 |
| Fig. 3b Mean Average (during XBT years) |
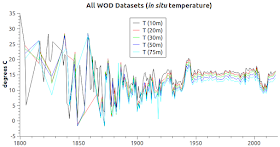 |
| Fig. 3c Mean Average of "T" (all years) |
That is why they were not contained in previous graphs of the WOD Datasets that displayed Conservative Temperature (CT) and Absolute Salinity (SA) values.
So, let me move on to further elaborate why this is of fundamental importance.
I have complained often about the mythic mantra that "thermal expansion is the main cause of sea level rise over the past century" as follows:
"Thermal expansion of pure water does not have the same thermodynamic events that the thermal expansion of sea water has.(On Thermal Expansion & Thermal Contraction - 36). Using drinking water to argue elements of seawater behavior is moronic.
Nevertheless, you can search the Internet and find videos of someone pouring pure water into a flask, making a mark on the flask, then heating the flask with a Bunsen Burner.
Then, after the water warms, they will put another mark on the flask ostensibly showing that the heat has caused the water to increase in volume.
Then they are apt to declare that this proves that thermal expansion is the major cause of sea level rise because "as water warms it expands."
The problem with this Mickey Mouse trick is that the pure water they use is at a temperature that is not below its maximum density temperature of 4 deg. C when they apply heat to the flask."
I have detailed how to build your own system, using the most advanced thermodynamic tools available (Build Your Own Thermosteric Computational System).
In closing, let me include the critical TEOS-10 functions when one is contemplating the calculation of thermosteric volume change in seawater (i.e. thermal expansion / contraction):
"Once we load the in situ values (t=in situ sea water temperature in Celsius, sp = in situ conductivity ("salinity"), and depth) we can calculate some fundamental TEOS-10 values.(ibid, Build Your Own Thermosteric Computational System). I will be generating thermal expansion / contraction graphs from the 1800's using all the WOD Datasets (except MBT and XBT) to the present in upcoming posts.
z = gsw_z_from_p (depth, lat);Before we move on to calculate thermosteric volume changes (not mass changes) based on sea water temperature changes, we must calculate the thermal expansion coefficient (tec):
p = gsw_p_from_z (z, lat);
sa = gsw_sa_from_sp (sp, p, lon, lat);
ct = gsw_ct_from_t (sa, t, p);
ctmd = gsw_ct_maxdensity (sa, p);
tec = gsw_alpha (sa, ct, p)In the following formula, let vc = volume change, vol = mass-unit volume of depth layer ("ocean slice") mentioned in Section III above, prev_ct = last year's conservative temperature, ct = this year's conservative temperature.
Now we can calculate thermosteric volume change with this formula:
vc = vol * (1 + (tec * ct - prev_ct))Since vc , like vol, is in cubic kilometers (km3), to convert vc into millimeters of sea level change (SLC), we divide vc by 361.841, which is the number of cubic kilometers per millimeter of SLC."
(Although, I may first get into some cultural phenomena posts seeing as how the USA is degenerating as fast as, or perhaps faster than, the Cryosphere.)
The next post in this series is here, the previous post in this series is here.
No comments:
Post a Comment